Альфа-бета-процедура

Теоретически, это эквивалентная минимаксу процедура, с помощью которой всегда получается такой же результат, но заметно быстрее, так как целые части дерева исключаются без проведения анализа. В основе этой процедуры лежит идея Дж. Маккарти об использовании двух переменных, обозначенных

и ? (1961 год).

Основная идея метода состоит в сравнении наилучших оценок, полученных для полностью изученных ветвей, с наилучшими предполагаемыми оценками для оставшихся. Можно показать, что при определенных условиях некоторые вычисления являются лишними. Рассмотрим идею отсечения на примере рис. 3.6. Предположим, позиция А полностью проанализирована и найдено значение ее оценки

. Допустим, что один ход из позиции Y приводит к позиции Z, оценка которой по методу минимакса равна z. Предположим, что z

. После анализа узла Z, когда справедливо соотношение y

s, ветви дерева, выходящие из узла Y, могут быть отброшены (альфа-отсечение).

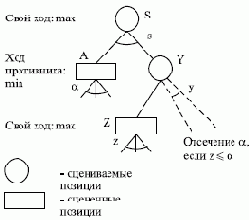
Рис. 3.6. - отсечение

Если мы захотим опуститься до узла Z, лежащего на уровне произвольной глубины, принадлежащей той же стороне, что и уровень S, то необходимо учитывать минимальное значение оценки ?, получаемой на ходах противника.

Отсечение типа ? можно выполнить всякий раз, когда оценка позиции, возникающая после хода противника, превышает значение ?. Алгоритм поиска строится так, что оценки своих ходов и ходов противника сравниваются при анализе дерева с величинами

и ? соответственно. В начале вычислений этим величинам присваиваются значения +? и -?, а затем, по мере продвижения к корню дерева, находится оценка начальной позиции и наилучший ход для одного из противников.

Правила вычисления

и ? в процессе поиска рекомендуются следующие:

у MAX вершины значение
равно наибольшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин;
у MIN вершины значение ? равно наименьшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин.

Правила прекращения поиска:

можно не проводить поиска на поддереве, растущем из всякой MIN вершины, у которой значение ? не превышает значения
всех ее родительских MAX вершин;
можно не проводить поиска на поддереве, растущем из всякой MAX вершины, у которой значение
не меньше значения ? всех ее родительских MIN вершин.

На рис. 3.7 показаны

-? отсечения для конкретного примера. Таким образом,

-?-алгоритм дает тот же результат, что и метод минимакса, но выполняется быстрее.

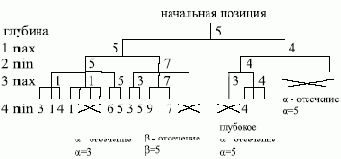
Рис. 3.7. a-b отсечение для конкретного примера

Использование алгоритмов эвристического поиска для поиска на графе И, ИЛИ выигрышной стратегии в более сложных задачах и играх (шашки, шахматы) не реален. По некоторым оценкам игровое дерево игры в шашки содержит 1040 вершин, в шахматах 10120 вершин. Если при игре в шашки для одной вершины требуется 1/3 наносекунды, то всего игрового времени потребуется 1021 веков. В таких случаях вводятся искусственные условия остановки, основанные на таких факторах, как наибольшая допустимая глубина вершин в дереве поиска или ограничения на время и объем памяти.

Многие из рассмотренных выше идей были использованы А. Ньюэллом, Дж. Шоу и Г. Саймоном в их программе GPS. Процесс работы GPS в общем воспроизводит методы решения задач, применяемые человеком: выдвигаются подцели, приближающие к решению; применяется эвристический метод (один, другой и т. д.), пока не будет получено решение. Попытки прекращаются, если получить решение не удается.

Программа STRIPS (STanford Research Institut Problem Solver) вырабатывает соответствующий порядок действий робота в зависимости от поставленной цели. Программа способна обучаться на опыте решения предыдущих задач. Большая часть игровых программ также обучается в процессе работы. Например, знаменитая шашечная программа Самюэля, выигравшая в 1974 году у чемпиона мира, "заучивала наизусть" выигранные партии и обобщала их для извлечения пользы из прошлого опыта. Программа HACHER Зуссмана, управляющая поведением робота, обучалась также и на ошибках.

Содержание раздела