Метод сопровождающего трехгранника.

Для записи обрабатываемой поверхности воспользуемся методом, описывающим перемещение подвижного трехгранника (???)i относительно системы координат (XYZ)д, в которой задается поверхность. Положение трехгранника задается матрицей вида (10.1), которая является универсальной как для описания поверхности, так и для описания кинематической схемы сложного пространственного механизма

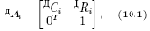
где

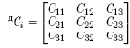
— подматрица направляющих косинусов осей подвижного трехгранника (???)i относительно осей координатной системы (XYZ)д, дRi=[xiyizi]T — вектор, определяющий положение i–й точки поверхности в системе координат (XYZ)д. Матрица (10.1) может быть представлена в табличной форме (таблица 11.1), в которой k — номер опорной точки линии, Cij - направляющие косинусы осей сопровождающего трехгранника (???)i относительно осей системыкоординат (XYZ)д, xi, yi, zi — координаты опорных точек траектории в системе координат (XYZ)д, ?i и ?i — соответственно радиус кривизны и кручения в опорной точке.

Таблица 11.1.

c11

c21

c31

c12

c22

c32

c13

c23

c33

...

Для задания траектории на поверхности также используется перемещающийся трехгранник, в котором направление движения по траектории совпадает с осью ?i. В зависимости от способа задания системы координат, относительно которой описывается обрабатываемая поверхность, и, соответственно, способа крепления детали, определяются алгоритмы управления манипуляционной системой. Кроме того, способ закрепления детали в захватном устройстве задаетколичество степеней подвижности манипулятора перемещения детали, необходимое для получения требуемой поверхности.

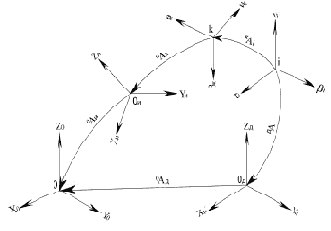
Рис. 11.2.

Предложенный метод описания геометрии обрабатываемой детали с применением сопровождающего трехгранника является обобщенным методом задания сложной поверхности. При анализе кинематики механизмов относительного манипулирования вводятся следующие координатные системы (рис. 11.2):

(XYZ)0 — неподвижная система координат;
(XYZ)д — система координат, связанная с местом крепления детали либо с ее базовыми поверхностями, относительно которых описывается обрабатываемая поверхность;
(XYZ)и — система координат, связанная с местом крепления инструмента, относительно которого описывается его режущая поверхность и положение режущей кромки;
(???)k — подвижный трехгранник, связанный с режущей кромкой и определяющий ее положение относительно (XYZ)и
(???)i — подвижный трехгранник, связанный с точками поверхности и определяющий их положение в системе координат (XYZ)д.

Введенные системы координат дают возможность алгоритмизировать процесс обработки наиболее экономичным образом и с единых позиций разрабатывать алгоритмы управления манипулятором.

Как было отмечено выше, математически обрабатываемая поверхность получается взаимным перемещением двух трехгранников — (???)i, связанного с поверхностью детали, и (???)k, связанного с режущей кромкой инструмента (рис. 11.2). Элементы матрицы kAi определяют перемещение режущей кромки относительно программного задания поверхности, иAk — положение режущей кромки в системе координат (XYZ) и дAi — положение программируемых опорных точек поверхности в системе координат детали, 0Aд и 1Aи — положение систем координат (XYZ)д и (XYZ)и относительно (XYZ)0.

Рассмотрим способы формирования матрицы описания обрабатываемой поверхности kAi при перемещении между опорными точками для различных типовых поверхностей. Для получения требуемой поверхности рассматривается случай перемещения детали относительно режущей поверхности. (Получение обрабатываемой поверхности возможно и при обратном движении инструмента относительно детали.)

Содержание раздела