в получении коэффициентов полиномов Лагранжа
Задача 1 состоит в получении коэффициентов полиномов Лагранжа по заданным координатам опорных точек поверхности. Интерполяционные полиномы Лагранжа одной переменной позволяют аппроксимировать функцию y=f(x) в системе координат детали (XYZ)д, задаваемую координатами опорных точек (xi,yi)
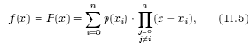
где коэффициенты полиномов Лагранжа p(xi) определяются через значения xi, yi в опорных точках
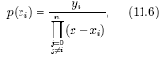
где i=0?n, j=0?n, n — степень полинома.
Полином Лагранжа двух переменных для поверхности, представленной на рис. 11.3, по аналогии с полиномом одной переменной имеет вид
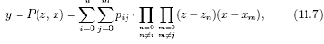
где i=[0?n] — количество опорных сечений поверхности вдоль оси Xд; j=[0?n] — количество опорных сечений поверхности вдоль оси Zд; pij — коэффициенты полинома, определяемые через координаты опорных точек поверхности.
Рассмотрим аппроксимацию поверхности полиномами Лагранжа второй степени.
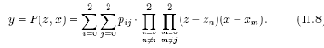
При интерполяции поверхности полиномами двух переменных необходимо, чтобы опорные точки поверхности (узлы интерполяции) образовывали сетку. Наиболее удобной является прямоугольная сетка с равномерным распределением клеток. В этом случае поверхность, представляемая координатами узлов прямоугольной сетки (рис. 11.3, а), в зависимости от расположения текущих координат (z,x) поверхности последовательно "накрывается" прямоугольником (рис. 11.3, б). При этом для более точной аппроксимации необходимо, чтобы текущие координаты поверхности (z,x) находились в области центра прямоугольника, ограниченного координатами
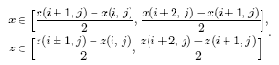
Последовательность выбора опорных точек, описывающих заданную ограниченную область поверхности, где проходит планируемая траектория, состоит в том, что все последующие опорные точки поверхности выбираются только после выхода i–й точки планируемой траектории из центра прямоугольника (рис. 11.3, б).
Постоянные коэффициенты полинома pij (11.8) определяются для каждого элемента поверхности через координаты известных опорных точек поверхности
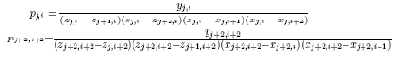
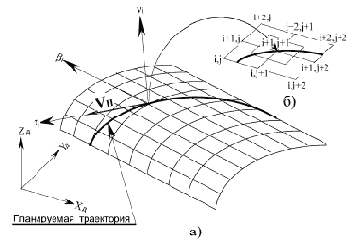
Рис. 11.3.
С учетом принятых обозначений полином (11.8) приводится к виду
y=a1z2x2+a2z2x+a3zx2+a4z2+a5x2+a6zx+a7z+a8x+a9, (11.9)
где коэффициенты ak вычисляются через постоянные pij и координаты опорных точек поверхности.
Задача 2 состоит в определении углов ориентации трехгранника (???)i относительно осей системы координат (XYZ)д. Для каждой i–й точки поверхности, используя уравнение (11.9), кроме текущих координат поверхности, вычисляются направляющие косинусы для осей трехгранника (???)i, связанного с поверхностью, которые представляют соответственно касательную, нормаль и бинормаль в каждой точке поверхности.
Для нахождения углов ориентации сопровождающего трехгранника (???)i в каждой точке траектории относительно осей системы координат (XYZ)д необходимо получить уравнение нормали в точке поверхности, касательной к траектории перемещения инструмента относительно детали, и уравнение бинормали.
Направляющие косинусы нормали (ось ?i) к поверхности в каждой точке траектории xiyizi определяются из уравнения (11.9)
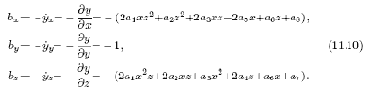
С учетом (11.10) направляющие косинусы для оси ?i в точке поверхности относительно осей системы координат (XYZ)д принимают вид
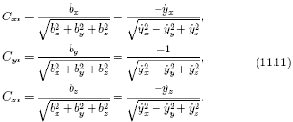
Направляющие косинусы для касательной (ось ?i) к траектории движения инструмента относительно детали определяется через частные производные от x, y, z по времени в i–й точке
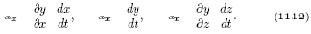
С учетом (11.12) получим
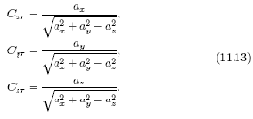
Направляющие косинусы для бинормали трехгранника (???)i — (ось ?i) определяются из векторного произведения
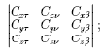
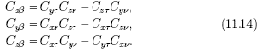
Таким образом, уравнения (11.11), (11.13) и (11.14) определяют ориентацию подвижного трехгранника (???)i относительно осей системы координат (XYZ)д.
Задача 3 состоит в нахождении элементов матрицы дAi(рис. 9.5), определяющей закон перемещения инструмента относительно детали. Элементы матрицы дAi
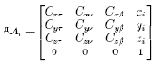
находятся на основе решения задач 1 и 2. Координаты xi, yi, zi представляют переменные x, y и z в полиноме Лагранжа (11.7), вычисляемые для каждой i–й точки траектории перемещения инструмента по поверхности детали. Направляющие косинусы Cx?, Cx?, Cx?, Cy?, Cy?, Cy?, Cz?, Cz?, Cz? определяются из уравнений (11.11), (11.13) и (11.14).
Для получения непрерывного перемещения по планируемой траектории с заданной скоростью Vп (рис. 11.3) ее координаты x и z задаются в параметрическом виде
x(t)=Vxt, z(t)=Vzt,
где скорости Vx и Vz для текущего шага вычисляются через значение Vп на предыдущем шаге
Vx=Cx Vп, VZ=CzVп.
Значения Cx и Cz определяются также на предыдущем шаге.
Подстановкой текущих координат x(t), z(t) в (11.9) вычисляется координата y(t) планируемой точки траектории, а также планируемые значения направляющих косинусов Cx?, Cx?, Cx?, Cy?, Cy?, Cy?, Cz?, Cz?, Cz?. Текущие элементы дAi вычисляются для каждой точки траектории с частотой задания координат x(t) и z(t).
Таким образом, метод, основанный на применении сопровождающего трехгранника, в сочетании с описанием обрабатываемой поверхности детали полиномами Лагранжа позволяет планировать закон перемещения инструмента и его ориентацию относительно детали для получения поверхностей, задаваемых координатами опорных точек.
