Погрешности выходного звена
Погрешности выходного звена будем рассматривать в системе координат (XYZ)П. Данные погрешности путем матричных преобразований можно получить в любой другой координатной системе. Определим связь межу погрешностями, представленными в системах (XYZ)i и (XYZ)П (рис. 13.2). С точностью до элементов первого порядка малости погрешности датчиков ?xдi,?yдi или ?zдi приводят к погрешностям вычисления линейных координат ?xп,?yп и ?zп
[?xп?yп?zп]T=пCдi[?xдi?yдi?zдi]T (13.2)
и погрешностям вычисления угловых координат
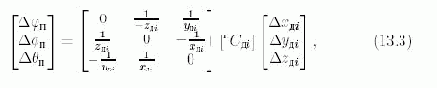
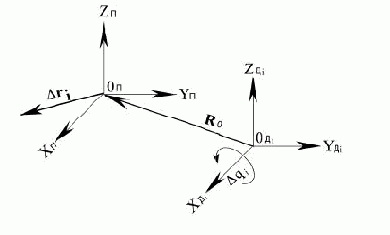
Рис. 13.2.
где [?xдi?yдi?zдi]T - вектор, определяющий положение точки 0дi в системе координат (XYZ)П (4-й столбец матрицы преобразования координат пAдi); пCдi - подматрица направляющих косинусов матрицы пAдi.
Как правило, датчики, расположенные в сочленениях звеньев, измеряют только одну из координат xдi,yдi или zдi, поэтому соответствующий данной координате столбец матрицы пCдi в (13.2) или в произведении матриц (13.3)
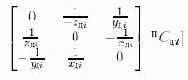
представляет коэффициенты в матрице KJ (13.1) при одной из координат xдi,yдi или zдi, измеряемой датчиком
[?xп?yп?zп]T=[K1дiK2дiK3дi]?дi (13.4)
Если датчик измеряет один из углов поворота вокруг оси Xдi,Yдi или Zдi, то погрешности ?


[?


Для каждой одной угловой координаты, измеряемой датчиком, коэффициенты KJ в (13.1) представляют столбец в матрице пCдi при этой координате
[?

Задача определения линейных погрешностей ?xп, ?yп и ?zп в системе координат (XYZ)П по заданным погрешностям датчиков, измеряющих только угловые координаты в сочленениях звеньев, имеет решение только при измерении одного из углов в системе (XYZ)дi. На рисунке 13.2 - это угол вращения относительно оси Xдi. Для этого случая связь линейных погрешностей в системе координат (XYZ)дi с угловой погрешностью датчиков по координате ?qi определяется из векторного произведения
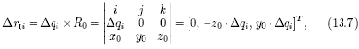
где R0=[x0y0z0]T - вектор, проведенный из 0дi в точку 0п.
Координаты R0 определяются из матрицы пAдi умножением четвертого столбца, взятого с противоположным знаком, на матрицу направляющих косинусов пCдi
[x0y0z0]T=пCдi[-xдi, -yдi, -zдi]T (13.8)
В зависимости от выбора направления оси, относительно которой измеряется угол вращения, погрешность ?qi в определителе (13.7) записывается во второй строке на первом месте для оси Xдi, на втором месте - для оси Yдi и на третьем - для оси Zдi.
Для определения линейной погрешности в системе координат выходного звена (XYZ)П необходимо ?rдi умножить на матрицу направляющих косинусов пCдi
[?xп?yп?zп]T=пCдi·?rдi (13.9)
Таким образом, уравнения (13.2)-(13.9) позволяют определять коэффициенты матрицы KJ (13.1), которые устанавливают взаимосвязь между линейными и угловыми погрешностями датчиков и погрешностями перемещения конечного звена механизма в системе координат (XYZ)П.
Надо отметить, что элементы матрицы пAдi, а следовательно и коэффициенты KJ в (13.1), являются функциями геометрических параметров механизма и измеряемых координат KJ=KJ(q,L), поэтому также вычисляются с погрешностями
KJ=KJ0(q,L)+?KJ(q,L) (13.10)
Подстановкой (13.1) в (13.10) получим
?R=KJ·?qJ=(KJ0+?KJ)?qJ=KJ0?qJ+?KJ?qJ (13.11)
Однако погрешность
?KJ?qJ=(?K/?q)?qJ?qi
является погрешностью второго порядка малости, поэтому для первого приближения данные погрешности можно принять равными нулю.
