Алгоритм проверки корректности поведения
Предположим, что нам даны конечная асинхронная модель поведения целевой системы ( P,


Для этого необходимо проверить существование пути ( e1, e2, …, en ) в автомате A, начинающегося в состоянии v0 и помеченного взаимодействиями из P так, чтобы это не противоречило частичному порядку π.
Асинхронная модель требований A = ( V, X, Y, Z, E ) задается асинхронной спецификацией { SpecSi | i = 1, …, k; k > 0 }

В данном разделе мы не будем рассматривать пути решения этой проблемы. Здесь мы будем считать, что нам задана вспомогательная функция γ : V x ( (X x Y)


γ( v, p ) = { v'


Но даже в этом случае для проверки корректности поведения требуется рассмотреть все возможные линеаризации асинхронной модели поведения и для каждой из них проверить существование соответствующего пути в автомате A.
Определение 12.
Линейный порядок < на частично-упорядоченном множестве ( P,






Для последующего рассмотрения введем вспомогательную функцию Г*, вычисляющую по состоянию в автомате и последовательности асинхронных взаимодействий, множество состояний автомата, достижимых из данного по последовательности дуг, помеченных данной последовательностью взаимодействий.
Формальное определение функции Г* следующее:
Г* ( v0, ( p1, p2, …, pn ) ) =

Г( V, p ) =
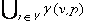
Лемма.
Для последовательности асинхронных взаимодействий ( p1, p2, …, pn ) существует путь ( e1, e2, …, en ) в автомате A, начинающийся в состоянии v0 и помеченный данными взаимодействиями, тогда и только тогда, когда Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Доказательство.
Действительно, пусть существует путь v0
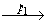
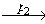
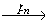

Базис индукции. (n = 1)
Итак, пусть v0
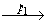



Шаг индукции.
Предположим, что мы доказали утверждение для путей длины n-1. Докажем его для n.
Пусть существует путь v0
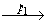
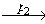
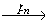

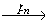




В обратную сторону.
Пусть Г*( v0, ( p1, p2, …, pn ) ) ≠ Ø. Докажем индукцией по n, что в автомате A существует путь v0
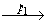
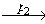
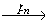
Базис индукции. (n = 1)
Пусть Г* ( v0, ( p1 ) ) ≠ Ø. Тогда существует v1

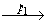
Шаг индукции.
Предположим, что мы доказали утверждение для n-1. Докажем его для n.
Пусть Г* ( v0, ( p1, p2, …, pn ) ) ≠ Ø.
Тогда




Предположим, что это не так.
То есть




Тогда Г* ( v0, ( p1, p2, …, pn ) ) = Г( … Г( Г* ( v0, ( p1, p2, …, pk ) ), pk+1 ), … pn ) =
=
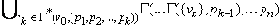
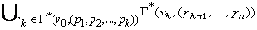
=
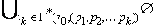
Данное утверждение верно и для k = 1. То есть найдется такое состояние v1

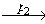
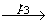
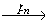
Так как v1

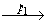
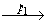
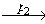
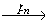
Как следует из леммы, проверка существования пути в автомате сводится к последовательному применению функции Г, вычислительная сложность которого сильно зависит от числа состояний, допускаемых моделью требований в качестве постсостояния перехода с заданными пресостоянием и асинхронным взаимодействием. В дальнейших оценках мы будем считать, что асинхронная модель требований допускает не более одного такого состояния, то есть модель является детерминированной.
Асинхронная модель требований A = ( V, X, Y, Z, E ) называется детерминированной, если для каждого состояния v





Для детерминированных моделей проверка существования пути, начинающегося в заданном состоянии v0 и помеченного заданной последовательностью взаимодействий ( p1, p2, …, pn ), в худшем случае сводится к n-кратному вычислению функции γ. Таким образом, сложность этой проверки оценивается сверху n-кратной сложностью вычисления функции γ.
Для оценки корректности асинхронной модели поведения такую проверку необходимо выполнить для каждой возможной линеаризации мультимножества асинхронных взаимодействий. А в худшем случае число линеаризаций составляет n!, где n - мощность множества P. То есть общая оценка сложности составляет n · n!.
Заметим, что многие линеаризации имеют общее начало. Этим свойством можно воспользоваться, чтобы не дублировать проверку существования путей, соответствующих общему началу линеаризаций.
Определим для множества P дерево возможных линеаризаций, как дерево, в котором
- из корня выходит n дуг, из вершин первого уровня - n-1 дуга, …, из вершин n-го уровня - 1 дуга и из вершин n+1-го уровня - ни одной дуги.
- каждая дуга помечена элементом из P,
- дуги, выходящие из вершины, путь к которой из корня дерева помечен последовательностью ( p1, p2, …, pk ), помечены элементами P, которые составляют множество Р \ { p1, p2, …, pk }.
Пример дерева возможных линеаризаций для P = { 1, 2, 3 } представлен на рисунке 11.
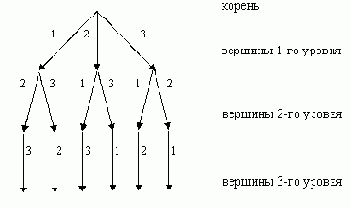
Рисунок 11. Дерево возможных линеаризаций для Р = { 1, 2, 3 }.
Заметим, что пути, ведущие из корня в листья, помечены последовательностями элементов из P, каждая из которых является линеаризацией множества P, а все вместе они образуют множество всех возможных линеаризаций.
Припишем к каждой вершине дерева возможных линеаризаций подмножество P, составленное из элементов { p1, p2, …, pk }, которыми помечен путь из корня дерева к данной вершине.
Деревом возможных линеаризаций частично-упорядоченного множества ( P,


Идеалами частично-упорядоченного множества ( P,






Лемма.
Пути из корня в листья дерева возможных линеаризаций частично-упорядоченного множества ( P,


Доказательство.
Покажем, что любой путь из корня в лист помечен последовательностью являющейся линеаризаций. Действительно, по построению дерева, любая такая последовательность является упорядочиванием всех элементов P. Покажем, что определяемый ею линейный порядок сохраняет исходный частичный порядок

Предположим, что это не так. То есть




Из того, что p2 < p1 следует, что дуга, помеченная p2, встречается в пути раньше, чем дуга, помеченная p1. Следовательно, к вершине, в которую ведет дуга, помеченная p2, приписано множество, содержащее p2 и не содержащее p1. Такое множество не является идеалом, то есть рассматриваемые дуги не могут принадлежать дереву возможных линеаризаций. Противоречие показывает, что наше предположение не верно и любая последовательность на пути из корня в лист является линеаризаций.
Докажем, что для любой линеаризации ( P,

Для этого мы рассмотрим путь в дереве возможных линеаризаций множества P, помеченный соответствующей последовательностью элементов ( p1, p2, …, pn ), и покажем, что этот путь будет присутствовать в дереве возможных линеаризаций частично-упорядоченного множества ( P,

Предположим, что это не так и одна из вершин этого пути была удалена из дерева. Это могло произойти только в случае, когда данная вершина принадлежит поддереву, к корню которого приписано множество, не являющееся идеалом ( P,


Это множество состоит из элементов, приписанных к пути из корня дерева в эту вершину. Так как такой путь в дереве единственен, то он совпадает с началом пути ( p1, p2, …, pn ). Следовательно,


То есть существуют такие i и j, что pi





Отсюда, i ≤ k < j


Если не дублировать проверку существования путей, соответствующих общему началу линеаризаций, то число необходимых вычислений функции γ будет совпадать с числом дуг в дереве возможных линеаризаций. Число дуг в дереве для множества размерностью n составляет:
n + n·(n-1) + … + n·(n-1)· … ·1 =
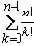
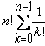
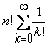
Основной сложностью в реализации этого алгоритма является организация перебора возможных линеаризаций асинхронной модели поведения ( P,

С другой стороны, существуют другие алгоритмы перебора перестановок, которые позволяют сократить затраты на проверку того, является ли очередная перестановка линеаризацией или нет. Но применение нетривиального перебора линеаризаций должно обеспечивать не только сложность O(n!), но и избегать перебора k! заведомо неподходящих перестановок, в тех случаях, когда известно, что (n-k)-ый элемент в какой-то перестановке нарушает условия линеаризации.
Алгоритм перебора линеаризаций, удовлетворяющий всем этим требованиям, был построен на основе алгоритма перебора перестановок 1.11, описанного в []. Этот алгоритм обеспечивает перебор перестановок таким образом, что каждая последующая перестановка отличается от предыдущей транспозицией одной пары элементов. В результате, проверка соответствия очередной перестановки условиям линеаризации требует в большинстве случаев константного времени. И в то же время, данный алгоритм позволяет избежать перебора k! заведомо неподходящих перестановок.
Алгоритм проверки корректности поведения, представленный ниже, основан на обходе дерева возможных линеаризаций в глубину. В нем используется следующая вспомогательная функция int B (int m , int i ), сложность вычисления которой ограничена константой:
int B(int m, int i) { if ((m%2 == 0) && (m > 2)) {if ( i < m-1 )
return i; else return m-2; }
else return m-1; }
Сам алгоритм представлен далее.
Алгоритм проверки корректности поведения.
Входные данные.
Асинхронная модель поведения ( P,

- массивом асинхронных взаимодействий P ( |P| = n );
- двухмерным массивом частичного порядка order[n,n]
- order[i,j] = 1, если P[i] P[j];

- order[i,j] = 0, в противном случае.
Асинхронная модель требований A = ( V, X, Y, Z, E ) задана функцией возможных постсостояний γ : V x ( (X x Y)


Начальное состояние v0

Данные алгоритма.
bound : Nat[n] := { n, n-1, …, 2, 1 }
массив счетчиков числа точек ветвления дерева возможных линеаризаций.
perm : Nat[n] := { 0, 1, …, n-1 }
массив, хранящий текущую перестановку взаимодействий.
current : Nat := 0
индекс текущего элемента перестановки.
path : (V-set)[n+1] := { {v0}, Ø, …, Ø }
массив множеств состояний текущего пути в модели требований. Для детерминированных моделей требований этот массив может быть заменен на массив состояний V, так как все его элементы будут множествами с размерностью не более 1.
processed : Nat := 0
индекс наибольшего элемента пути, содержащего актуальное множество состояний модели требований.
order_failed : Bool := false
флаг, содержащий истинное значение только в том случае, когда текущая перестановка не является линеаризацией частичного порядка

current2 : Nat := 0
вспомогательная переменная для хранения индекса второго взаимодействий, участвовавшего в последней транспозиции.
tmp : Nat := 0
вспомогательная переменная.
j : Nat := 0
вспомогательная переменная.
Алгоритм.
- Алгоритм вычисляет является ли текущая перестановка perm линеаризацией частичного порядка , записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку
 , или к шагу 3 - в противном случае. При этом предполагается, что упорядочение P[perm[0]], …, P[perm[current]] не противоречит частичному порядку
, или к шагу 3 - в противном случае. При этом предполагается, что упорядочение P[perm[0]], …, P[perm[current]] не противоречит частичному порядку и поэтому достаточно проверить элементы перестановки, начиная с current.
и поэтому достаточно проверить элементы перестановки, начиная с current.
for(;current<n-1;current++) {for(j=current+1;j<n;j++) {if (order[perm[j],perm[current]]) {order_failed = true; goto 3; } } }
order_failed = false;
- Алгоритм строит пути в модели требований, соответствующие последовательности взаимодействий в текущей перестановке, заполняя массив path. При этом предполагается, что начальные отрезки пути path[0], …, path[processed] уже построены ранее. Если на одном из шагов множество состояний модели требований оказывается пустым, то алгоритм переходит к шагу problem, установив значение переменной current равное индексу элемента перестановки для которого было получено пустое множество. Если же path[n] ≠ Ø, то алгоритм завершает свою работу с положительным вердиктом. Найдена линеаризация ( P[perm[0]], P[perm[1]],…, P[perm[n-1]] ), для которой множество Г*( v0, ( P[perm[0]], P[perm[1]], …, P[perm[n-1]] ) ) = path[n] не пусто.
for(;processed<n;processed++) {path[processed+1] = Ø; foreach v : V in path[processed] path[processed+1] = path[processed+1]γ( v, P[perm[processed]] ); if (path[processed+1] == Ø) {current = processed; for(j=current+1;j<n;j++) bound[j] = n-j; goto 3; } }
КОНЕЦ ( асинхронная модель поведения является корректной относительно данной асинхронной модели требований)
- Если индекс текущего элемента перестановки больше либо равен n-2 или , то алгоритм переходит к шагу 9.
if ((current ≥ n-2) || (bound[current] == 1)) goto 9;
- Если индекс текущего элемента перестановки является нечетным при обратной нумерации элементов перестановки [n-1 0, …, 0
 n-1], то алгоритм переходит к шагу 7.
n-1], то алгоритм переходит к шагу 7.
if ((n-current) % 2 == 0) goto 7;
- Алгоритм осуществляет циклический сдвиг хвоста перестановки на единицу
perm[current+2]perm[current+1] … perm[n-1] perm[n-2] perm[current+1]
perm[n-2] perm[current+1] perm[n-1]
perm[n-1]
tmp = perm[current+1]; for(j=current+1;j<n-1;j++) perm[j] = perm[j+1]; perm[n-1] = tmp;
- Если предыдущая перестановка не противоречила частичному порядку , то алгоритм вычисляет не противоречит ли новая перестановка этому порядку, записывает результат в переменную order_failed и переходит к шагу 9.

if (!order_failed) {for(j=current+1;j<n-1;j++) {if (order[perm[n-1],perm[j]]) {order_failed = true; break; } } }
goto 9;
- Алгоритм осуществляет транспозицию элементов перестановки с индексами current+1 и current+2.
tmp = perm[current+1]; perm[current+1] = perm[current+2]; perm[current+2] = tmp;
- Если предыдущая перестановка не противоречила частичному порядку , то алгоритм вычисляет не противоречит ли новая перестановка этому порядку и записывает результат в переменную order_failed.

if (!order_failed) {if (order[perm[current+2],perm[current+1]]) order_failed = true; }
- Если текущий счетчик числа точек ветвления равен 1, то алгоритм переходит к шагу 14.
if (bound[current] == 1) goto 14;
- Алгоритм осуществляет транспозицию элементов перестановки с индексами current и n-B(n-current,n-current-bound[current]+1), сохраняя индекс второго элемента в переменной current2.
current2 = n-B(n-current,n-current-bound[current]+1); tmp = perm[current]; perm[current] = perm[current2]; perm[current2] = tmp;
- Алгоритм уменьшает текущий счетчик числа точек ветвления на единицу.
bound[current]--;
- Если предыдущая перестановка противоречила частичному порядку ;, то алгоритм переходит к шагу 1.

if (order_failed) goto 1;
- В противном случае алгоритм вычисляет, не противоречит ли новая перестановка частичному порядку , записывает результат в переменную order_failed и переходит к шагу 2, если текущая перестановка не противоречит частичному порядку
 , или к шагу 3 - в противном случае. В последнем случае алгоритм устанавливает значение переменной current равное наименьшему индексу элемента перестановки, для которого нарушается условие линеаризации.
, или к шагу 3 - в противном случае. В последнем случае алгоритм устанавливает значение переменной current равное наименьшему индексу элемента перестановки, для которого нарушается условие линеаризации.
for(j=current+1;j<=current2;j++) {if (order[perm[j],perm[current]]) {order_failed = true; goto 3; } }
for(j=current+1;j<current2;j++) {if (order[perm[current2],perm[j]]) {order_failed = true; current = j; goto 3; } }
goto 2;
- Если индекс текущего элемента перестановки равен 0, то алгоритм завершает свою работу с отрицательным вердиктом.
if (current == 0) КОНЕЦ (асинхронная модель поведения является не корректной относительно данной асинхронной модели требований)
- В противном случае алгоритм переинициализирует текущий счетчик числа точек ветвления и уменьшает индекс текущего элемента перестановки на единицу.
bound[current] = n-current; current--;
- Если индекс текущего элемента перестановки оказался меньше индекса наибольшего элемента пути, содержащего актуальное множество состояний модели требований, то значение последнего устанавливается равным значению первого.
if (current < processed) processed = current;
- Алгоритм переходит к шагу 9.
goto 9;
Доказательство корректности данного алгоритма представлено в [].
Частичный порядокмодели поведения рассматривается в алгоритме в виде двухмерной матрицы n x n, содержащей значение 1 для пар принадлежащих частичному порядку и 0 - в противном случае. Для построения этой матрицы на основе моделей каналов и временных меток можно использовать алгоритм построения транзитивного замыкания Уоршала, который требует O(n3 ) операций [].Существуют также алгоритмы построения транзитивного замыкания с лучшей оценкой (например, O(nlog 7·log n)), однако они имеют преимущества только при очень больших значениях n.
Обратим внимание на тот факт, что оценка сложности алгоритма O(n!) получена для класса детерминированных моделей поведения, для недетерминированных моделей сложность становится еще больше. Но даже при использовании детерминированных моделей требования применимость алгоритма сильно ограничена: при числе взаимодействий, превышающем несколько десятков время работы становится неприемлемо большим. Поэтому при применении рассматриваемого метода необходимо учитывать имеющиеся ограничения на размерность модели поведения, участвующей в задаче оценки корректности.
Содержание раздела
