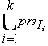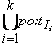Описание модели требований

Рассмотрим подход программных контрактов более детально и определим способ описания модели требований, применяемый в технологии UniTesK. Сигнатурой интерфейсной операции I называется тройка ( In, Out, Var ), где

• In = { xi | i = 1, …, in(I) ; in(I) ≥ 0 } - упорядоченный набор входных параметров операции,
• Out = { yi | i = 1, …, out(I) ; out(I) ≥ 0 } - упорядоченный набор выходных параметров операции,
• Var = { vi | i = 1, …, var(I) ; var(I) ≥ 0 } - набор переменных состояния, к которым обращается данная операция.

Каждый входной параметр xi может принимать значения из непустого множества допустимых значений Xi, каждый выходной параметр yi может принимать значения из непустого множества допустимых значений Yi, а каждая переменная состояния vi может принимать значения из непустого множества допустимых значений Vi. Эти непустые множества допустимых значений далее будут называться типами параметров и переменных.

Рассмотрим пример операции вычисления квадратного корня. Сигнатурой этой операции является тройка ( { x1 }, { y1 }, {} ). Множеством допустимых значений единственного входного параметра x1 и единственного выходного параметра y1 является множество действительных чисел R. Пустое множество переменных состояния означает, что данная операция никак не зависит ни от одной переменной состояния.

Введем следующие обозначения:

XI = X1 x … x Xin(I), если in(I) > 0, и XI = { ε }, в противном случае;

YI = Y1 x … x Yout(I), если out(I) > 0, и YI = { ε }, в противном случае;

VI = V1 x … x Vvar(I), если var(I) > 0, и VI = { ε }, в противном случае.

Спецификацией интерфейсной операции I с сигнатурой ( In, Out, Var ) называется пара предикатов ( preI, postI ), в которой

• preI - предикат на множестве VI x XI, называемый предусловием,
• postI - предикат на множестве VI x XI x YI x VI, называемый постусловием.

Спецификация интерфейсной операции утверждает, что если презначения переменных состояния и значения входных параметров удовлетворяют предусловию, то значения выходных параметров и постзначения переменных состояния должны удовлетворять постусловию для данных презначений переменных состояния и значений входных параметров.
Например, спецификацию операции вычисления квадратного корня ( presqrt, postsqrt ) можно задать следующим образом:


presqrt ( v, x1 ) ≡ (x1 ≥ 0)
postsqrt ( v, x1, y1, v' ) ≡ &#x007C; x1 - y12 &#x007C; < εпогр
Здесь, как и ранее, εпогр обозначает некоторое положительное действительное число.
Спецификацией целевой системы называется непустой набор спецификаций ее интерфейсных операций &#x007B; SpecIi &#x007C; i = 1, …, k; k > 0 &#x007D;.
В технологии UniTesK для описания требований к функциональности целевой системы (модели требований) также используется подход программных контрактов. Описание модели требований задается в виде спецификации Spec &#x007B; SpecIi &#x007C; i = 1, …, k &#x007D;, а соответствующая ей модель требований MR[Spec] ( V, X, Y, E ) определяется согласно следующим правилам:

1. Если в спецификации присутствует хотя бы одна переменная состояния, то множество состояний V является декартовым произведением множеств допустимых значений всех переменных состояния
   V=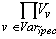
   
   ,
   
   где VarSpec является объединением переменных состояния всех интерфейсных операций, принадлежащих спецификации
   VarSpec =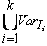
   
   .
2. 
   Если в спецификации не участвует ни одной переменной состояния, то множество состояний состоит из единственного элемента ε:
   V &#x007B; ε &#x007D;.
3. 
   Множество стимулов X является дизъюнктивным объединением декартовых произведений множеств допустимых значений входных параметров всех интерфейсных операций спецификации
   X =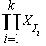
   
   .
   Мы будем считать, что каждый элемент дизъюнктивного объединения помечается именем интерфейсной операции и таким образом эти элементы не пересекаются между собой.
4. 
   
   
   Множество реакций Y является дизъюнктивным объединением декартовых произведений множеств допустимых значений выходных параметров всех интерфейсных операций спецификации
   Y =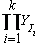
   
   .
   Мы будем считать, что каждый элемент дизъюнктивного объединения помечается именем интерфейсной операции и таким образом эти элементы не пересекаются между собой.
5. 
   Множество переходов E состоит из всех переходов, удовлетворяющих обобщенным предусловию и постусловию спецификации
   E = &#x007B; ( v, x, y, v' )
   
   V x X x Y x V &#x007C; pre( v, x )
   
   post( v, x, y, v' ) &#x007D;,
   
   где предикат pre =
   
   , а предикат post =
   

Содержание раздела

---

---